doi.org/10.15178/va.2017.140.45-54

RESEARCH

USE OF REPETITIVE PERMUTATION AS BINOMIAL EXPERIMENT TEACHING

USO DE LA PERMUTACIÓN CON REPETICIÓN COMO ENSEÑANZA DE EXPERIMENTOS BINOMIALES

USO DA PERMUTAÇÃO COM REPETIÇÃO COMO ENSINAMENTO DE EXPERIMENTOS BINOMIALES

Antonio José Boada¹ Bachelor of Education in Physics and Mathematics. Specialist in Computational Statistics. Master of Finance. Author and speaker at over 30 international refereed and indexed congresses. Author of more than 10 articles in refereed and indexed scientific journals. Professional with experience in Financing, Marketing, Demand Planning & Supply Chain. Specialist in Companies with Style of Direct Sale Style. Handling Moodle & Sakai virtual teaching tools. Educational Classification, Assessment and Entry at Higher Education. Virtual Distance Teaching and use of ICTs. Venezuelan, emigrated to Colombia. https://scholar.google.es/citations?user=Zv0EdDoAAAAJ&hl=es

¹CEIPA Business School. Medellín. Colombia

ABSTRACT

This article presents the reader two (2) ways of education for Experiments Bernoulli “Success - Failure” consolidated in the Probabilistic Binomial Distribution and explained from two (2) counting concepts: with repetition and without repetition.
Binomial Distribution, conceived as a discrete probabilistic distribution of successes and failures (experiments of Bernoulli), presents its most important characteristic in the counting of scenarios, determined by an expression determined by several authors as combinatorial number without repetition, when it is feasible to present it also as a permutation with repetition in two (2) scenarios, success and failure.
It is interesting to analyze the numerical coincidence between the use of permutation with repetition and the combinatorial number without repetition, promoting explanatory arguments to support teachers for two contexts of teaching - learning for the binomial distribution; on the one hand, the traditional method of combinatorial number without repetition, in a probabilistic distribution with independent events and, on the other hand, by way of a method of analogous counting to the Probabilistic Multinomial Distribution that presents a binding process between independent Bernoulli trials, by counting the events of the sample space through permutation with repetition, particularized for the case of 2 complementary scenarios (success and failure).
This is why every educator should know and manage both contexts of teaching - learning for Binomial Distribution, in order to enhance the teaching strategies necessary to contemplate the combinatorial theory with repetition or with replacement, with the option of permutations with repetition if required.

KEYWORDS: Permutation, Bernoulli Experiments, Binomial Probabilistic Distribution, Combinatorial Theory, Permutation with Repetition

RESUMEN

Mediante este artículo, se expone al lector dos (2) formas de enseñanza para los Experimentos Bernoulli “Éxito – Fracaso”, consolidadas en la Distribución Probabilística Binomial y explicados desde dos (2) concepciones de conteo: con repetición y sin repetición.
La Distribución Binomial, concebida como una distribución probabilística discreta de éxitos y fracasos (experimentos de Bernoulli), presenta su característica más importante en el conteo de escenarios, determinado por una expresión que diversos autores han determinado como número combinatorio sin repetición, cuando es factible exponerlo también como una permutación con repetición en dos (2) escenarios, de éxito y fracaso.
La coincidencia numérica entre el uso de la permutación con repetición y el número combinatorio sin repetición, resulta interesante de analizar, propiciando argumentos explicativos que pudieran apoyar al docente para dos contextos de enseñanza – aprendizaje para la Distribución Binomial; por un lado, el método tradicional de número combinatorio sin repetición, en una distribución probabilística con sucesos independientes; y por el otro mediante un método de conteo análogo a la Distribución Probabilística Multinomial y que expone un proceso de enlace entre los ensayos independientes Bernoulli, mediante el conteo de los eventos del espacio muestral mediante una permutación con repetición, particularizado para el caso de 2 escenarios complementarios (éxito y fracaso).
Es por ello, que todo educador, debe conocer y manejar ambos contextos de enseñanza – aprendizaje para la Distribución Binomial, a fin de potenciar las estrategias pedagógicas necesarias para contemplar la teoría combinatoria con repetición o con reemplazo, mediante la opción de permutaciones con repetición en caso de ser requerida.

PALABRAS CLAVE: Permutación, Experimentos de Bernoulli, Distribución Probabilística Binomial, Teoría Combinatoria, Permutación con Repetición

RESUMO

Mediante este artigo, se expõe ao leitor duas formas de ensinamento para os Experimentos Bernoulli ¨Exito-Fracasso¨, consolidados na Distribuição Probabilista Binomial e explicados desde duas concepções de contagem: com repetição e sem repetição. A distribuição Binomial concebida como uma distribuição probabilística discreta de êxitos e fracassos (experimentos de Bernoulli) apresenta sua característica mais importante na contagem de cenários, usado por uma expressão que diversos autores determinaram como número combinatório sem repetição quando é viável expor também como uma permutação com repetição em dois cenários, de êxito e fracasso. A coincidência numérica entre o uso da permutação com repetição e o número combinatório sem repetição, resulta interessante de analisar, propiciando argumentos explicativos que puderam apoiar ao docente para dois contextos de ensinamento – aprendizagem para a Distribuição Binomial; por um lado, o método tradicional de números combinatórios sem repetição, em uma distribuição probabilística com sucessos independentes; e por outro lado, mediante um método de contagem análogo a Distribuição Probabilística Multinomial e que expõe um processo de enlace entre os ensaios independentes Bernoulli, mediante a contagem dos eventos do espaço de amostras mediante uma permutação com repetição, particularizado para o caso de dois cenários complementários (êxito e fracasso).
É por isso que todo educador deve conhecer e manejar ambos contextos de ensinamento – aprendizagem para a Distribuição Binomial, afim de potenciar as estratégias pedagógicas necessárias para contemplar a teoria combinatória com repetição ou com substituição, mediante opção de permutações com repetições em caso de ser requerida.

PALAVRAS CHAVE: Permutação, Experimentos de Bernoulli, Distribuição Probabilística Binomial, Teoria Combinatória, Permutação com Repetição

Received: 14/03/2017
Accepted: 08/05/2017
Published: 15/09/2017

Correspondence: Antonio José Boada. antonio_boada@virtual.ceipa.edu.co

1. INTRODUCTION

In any randomized experiment, the results are presented at random; thus, it is called a random variable. Each value of the random variable is related to a probability indicating the possibility of a given result. (Lind, 2012). In this sense, the random variable presents the amount resulting from an experiment that, by chance, can take different values.
The binomial probability distribution is a discrete probability distribution that occurs very frequently. One of its features is that there are only two possible outcomes in a given trial of the experiment. The results are mutually exclusive, which means that the answer to a question of true or false cannot be both true and false at the same time. (Lind, 2012). Likewise, a feature of the binomial distribution is that each trial is independent of any other. Being independent means that there are no patterns in the trials. The result of a particular trial does not influence the outcome of another trial.
The Binomial Distribution presents the evaluation of a series of trials in Bernoulli experiments, quantified by a combinatorial number without repetition, an aspect that can hinder the teaching process, since Bernoulli experiments are calculated in independent scenarios, where there is repetition.
Under the concept of Binomial Distribution, (Shao, 1967 p-274), a deduction of the formula is given by an example of extracting two (2) white balls in three (3) extractions with replacement, under a universe of a bag with five (5) balls, where one is white and four (4) are black. In this respect, Shao correctly deduces the probability of “success”, corresponding to 1/5, and that of failure 4/5; this with the later purpose of establishing the scenario where two white balls are finally extracted in 3 extractions, which would result in (1/5) (1/5) (4/5), under the combination of results BBN, BNB, NBB (ie 3 options where it is possible to obtain 2 white balls and a black one). However, Shao defines the calculation of these 3 options as a combinatorial number without repetition nCk, where “n” presents the number of extractions (3) and “k” the number of occurrences of the event “white ball” (2). This is an aspect that can pedagogically generate interpretative problems in the teaching process, since the number of occurrences “k” is not an element without repetition, but rather the opposite, it can be a permutation with aspects (3 extractions) that are repeated (2 white balls), which would present the use of permutation with repetition.
In this sense, taking the example above, it may be difficult for the teacher to consider case quantification by a combinatorial number without repetition, when it can easily be represented as permutation with repetition, particularized to two (2) scenarios: Success and Failure.
The combinatorial theory presents two (2) conceptions: with repetition and without repetition. As its name implies, with repetition means that the terms can reappear or when the number of events is constant, that is, the universe does not vary with the extraction (Diaz, 2013), as in the case of independent binomial events: 3 faces and 4 seals when you toss a coin 7 times.
Several authors such as Walpole, 1998 and Webster, 2003, try to explain this misrepresentation pedagogically by arguing that the combinatorial number without repetition nCk corresponds to the count of “n” Bernoulli experiments, to select “k” cases where there are “k” successes, as If it were a case of combinatorial without repetition, but it turns out that under this conception, a reduction of the original sample space (universe of “n” Bernoulli experiments) should occur, an aspect that does not happen, since it was always “n” Bernoulli experiments, and they were always “k” successes, the only thing that has actually changed is the order in which successes are valued in various Bernoulli trials.
A Binomial Distribution will always try to count the independent Bernoulli experiments, and this article presents a proposal to make it through the use of permutations with repetition, that can model the number of anagrams of the independent cases EEE... EFFF... F, where they have “K” E (success) experiments and there are “n-k” F (Failure) experiments.

2. OBJECTIVE

Mathematically check that the counting expression used by a Binomial Probabilistic Distribution can be represented by permutation with repetition of “n” Bernoulli experiments. By means of this objective, we seek to promote the use of permutation with repetition, and to present to the teacher a new option of teaching the binomial distribution from the perspective of “n” independent Bernoulli experiments.

3. FRAME OF REFERENCE

3.1. Combinatorial number without repetition

The combinatorial number, or combination without repetition, expresses the count of ways to choose “k” elements within the possible “n” cases, regardless of the order of selection.

The combinations are all subsets of “k” elements that can be formed out of a set of “n” objects, and where a combination with the same elements is not another combination, but is the same, even if the elements are found in different order. (Díaz, 2013).
In the case of a combinatorial number without repetition, the presence of dependent events is fundamental, since the universe of elements is modified according to the selection of “successful” elements that are taken into consideration. As its name implies, it should be used in dependent counting elements (without repetition), and not in independent or repetitive counting scenarios (as in the case of as Binomial distribution).

3.2. Permutation with repetition

Permutation with repetition expresses a way to quantify the possible positions of the events, excluding those that have the same characteristics.

Where “n” corresponds to the total number of cases, while “ki” represent the classifications performed according to the characteristics to be segmented (which may be success and failure for the binomial case); thus. (Meyer, 1999)
It is always necessary to establish the differentiation between the combinatorial theory with repetition (independent or with replacement), vs the combinatorial theory without repetition (dependent or without replacement). Some authors, such as Anderson, 2016, express a single approach to the combinatorial theory without repetition (without stating the existence of another way of counting). Also, authors such as Walpole, 1998 (p-121) present permutation with repetition like a combinatorial number of diverse “groups”.

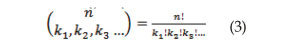
However, regardless of those presented by different authors, the combinatorial theory with repetition presents a set of tools that can be used and applied in all those sets where it is possible to repeat elements.
Under this conception, permutation with repetition presents an excellent counting way for independent scenarios, where the universe does not vary with the selection of scenarios; therefore, it can be applied directly to the count of events “number of successful events vs number of unsuccessful events”, becoming an ideal tool to teach probabilistic distributions of independent experiments, such as Binomial Distribution.
By means of permutation with repetition (number of times that cases of success are repeated and number of times that cases of failure are repeated), it is possible to use the same and synergistic teaching theory (with repetition) in Bernoulli events, which are clearly independent in their nature.

3.3. Similarity between permutation with repetition and the combinatorial number without repetition

When there are two (2) features to be segmented, such as success and failure, the formula of permutation with repetition matches the formula of combinatorial number without repetition. Recalling that, therefore, if k1 + k2 = n, then k2 = n - k1

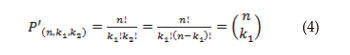
For this reason, the count of Bernoulli experiments, which is a simple problem of permutation with repetition (a particular case for 2 scenarios), has been misrepresented as a combinatorial number without repetition, with few pedagogical arguments to explain its origin. (Boada, 2001).
Some authors explain this misrepresentation by arguing that it corresponds to the count of “n” Bernoulli experiments, to select “k” cases where there are “k” successes (Diaz, 2013, Page 152), as if it were a case of a combinatorial without repetition, but it turns out that under this conception there is no decrease or alteration of the universe or the original sample space, since they were always “n” Bernoulli experiments, and they were always “k” successes, the only thing that has actually changed is the order in which successes are valued in the different Bernoulli trials. This explanation is incongruent, in a probabilistic distribution the main stronghold of which is the independence of Bernoulli experiments, and where its sample space should not have any alterations.
A Binomial Distribution will always seek to quantify the number of Bernoulli experiments, which can be modeled according to the number of anagrams of the independent “n” cases EEE... EFFF... F, where “k” experiments of E (success) are defined and it has “n-k” experiments of F (Failure).

4. DISCUSSION

4.1. Binomial distribution, analysis from 2 perspectives

Binomial Distribution is a discrete probability distribution that quantifies the number of successes in a sequence of ‘n’ Bernoulli trials independent of each other, with a fixed ‘p’ probability of occurrence of success. (Webster, 2003)
If we consider an experiment, and let A be a random event with the experiment, we can suppose that P (A) = p, and therefore (as it is a Bernoulli experiment) P (A) = 1 - p. Then, considering “n” independent repetitions of the experiment, we generate the sample space in all possible sequences as A and A occur. Also, it is assumed that P (A) = p is constant for all the repetitions (characteristic of independence between events). Given these premises, we can define a random variable X = Number of times event A occurred, given the parameters “n” and “p”. (Meyer, 1999)
Under this definition, the random variable X corresponds to a Binomial variable, with the parameters “n” and “p”, and the values of which are 0, 1, 2, 3,..., n. Where individual and independent repetitions of the experiments are called Bernoulli trials.

In this sense, the expression

Quantifies the number of Bernoulli trials where Successes (p) and Failures (1 – p) can be combined in “n” possible options. This expression is in line with the definition and use of the previously explained permutation with repetition, and not as a combinatorial number without repetition, which is usually placed in the statistical text books.

Let’s analyze below a simple example of the launch of “n” dice.

4.2. Multinomial Distribution.

Likewise, when the Multinomial distribution is analyzed, in this case, the presence of cases through generalized permutation with repetition for the diversity of cases appears in a quantified effect.
We consider an experiment, its sample space S, and a partition of S in “k” mutually exclusive events A1, A2, A3,..., Ak, and we consider “n” independent repetitions of the experiments. Let pi = P (Ai) and let us assume that pi remains constant during all the repetitions of each event, then

and the following theorem is defined, which gives life to the Multinomial Distribution.

If Xi, i = 1, 2, 3,..., k are defined under the previous precepts, then,

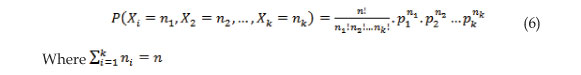
It should be noted that Xi, are not independent variables, since the sum is equal to the total number of data. (Meyer, 1999).

5. CONCLUSIONS

By means of this article, we can show a new teaching perspective for Binomial Discrete Probability Distribution, as a function of a series of independent Bernoulli trials, quantified by means of a theory of counting with repetition, through the use of permutation with repetition, particularized for the case of 2 complementary scenarios (success and failure).
At the level of the teaching of Binomial Distribution, this new way establishes a synergy with the conception of independence of Bernoulli experiments, since this new perspective presents a combinatorial theory of count for independent events (with repetition or with replacement), through the option of permutations with repetition.
Over the years, the use, management and explanation of the combinatorial theory with repetition has been relegated in the teaching of statistics, giving greater prominence to the combinatorial theory without repetition. This absence has made it possible to promote the teaching of binomial distribution under a single conception, without realizing that there is another way of explaining, not only the Binomial Distribution, but also the Multinomial Distribution, through the same theory of combinatorial counting with repetition.
By means of this article, the reader will be able to visualize the presence of two (2) ways of teaching for the counting of scenarios in a Binomial Probabilistic Distribution:
1. The traditional explanation using a combinatorial number without repetition nCk corresponds to the count of “n” Bernoulli experiments, to select “k” cases where there are “k” successes.
2. A new explanation through the use of permutation with repetition, where the original sample space (Bernoulli universe of experiments) and “k” successes are invariant, only the order in which successes are valued in the different Bernoulli trials changes.

REFERENCES

1. Anderson DR, Dennis JS, Thomas AW (2016). Estadística para Negocios y Economía. Londres: Cengage Learning.
2. Boada A (2001). Uso de la Permutación con Repetición, como Herramienta para la Enseñanza de la Probabilidad. Matanzas, Cuba: COMAT’01, Universidad de Matanzas.
3. Díaz-Mata A (2013). Estadística aplicada a la administración y la economía. McGraw-Hill Interamericana.
4. Douglas-Lind A (2012). Estadística aplicada a los negocios y la economía. McGraw-Hill Interamericana.
5. Meyer P (1999). Probabilidad y Aplicaciones Estadísticas. Addisson: Wesley Iberoamericana.
6. Shao-Stephen P (1967). Estadística para Economistas y Administradores de Empresas. México: Herrero Hermanos, Sucs.
7. Walpole R, Raymond M, Sharon M (1999). Probabilidad y estadística para ingenieros. Pearson Educación.
8. Webster-Allen L (2003). Estadística aplicada a los negocios y la economía. Bogotá: Mc Graw Hill.